Kaprekar's Constant

The teacher and mathematician D.R. Kaprekar D.R. Kaprekar (1905-1986) noticed that for arbitrary four-digit numbers, performing the following procedure (almost) always brings you to the same result: 6174.

1. Take the digits of the starting number (say, 8273) and re-arrange them from largest to smallest (e.g. 8273 → 8732)
2. Take the digits of the starting number and re-arrange them a second time, this time from smallest to largest (e.g. 8273 → 2378)
3. Subtract the number found in step 2 from the number found in step 1 (e.g. 8732 - 2378 = 6354)
4. Repeat steps 1 through 3 with the difference you just found

If we agree to pad any intermediate results less than 1000 with leading zeros, the only numbers for which this procedure does not work are numbers made up of the same digit repeated four times: 0000, 1111, 2222, etc. Performing the procedure with 6174 just gives you 6174 again.

The same procedure works for three-digit numbers, with a convergence point of 495.

Challenge

Write a program that reads a file called "input.txt" of starting values and writes a file called "output.txt" with the sequences generated from those values. Each line of "input.txt" contains a single positive integer. Validate the number (e.g. make sure it has the right number of digits and is not composed of one repeated digit like 333 or 9999) and calculate the Kaprekar sequence starting at that number. Write the sequence to the output file or write an error message if the input was invalid.

Implementation Notes

In C++, you can use sort() to re-order the digits if you first put them into an array or vector. sort() is in the algorithm library.

In Python, you can use sort() to re-order the digits if you first put them into a list. Although sort() is not strictly a built-in function, it is part of the list object, which is built-in.

A simple way to detect numbers like 222 or 5555 in either language is with the modulo operator because they are multiples of 111 and 1111, respectively.

Test Vectors

You can use this file as your input.

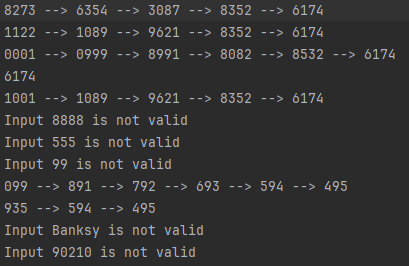
Your program should produce something like this as your output.

Takeaways

In this challenge, you had to break numbers down into their constituent digits, manipulate those digits, and then re-assemble them back into numbers. You had to check whether inputs were valid and worry about padding numbers to the proper width. You may have had to convert between strings containing numeric characters and the values those string represented. All these are tedious and error-prone operations, but they arise frequently and are extremely important. Well done!