Analysis: The Triangle
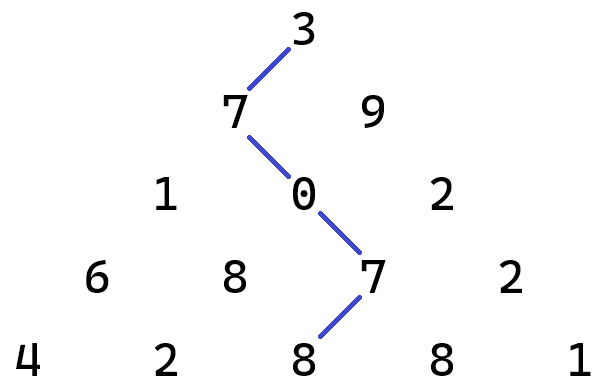
This task asks you consider all possible paths from the top to the bottom of a number triangle, identifying the highest sum formed by adding all the numbers along a path. For the arbitrary five-row number triangle that appears in Figure 1, we have illustrated one possible pathway. The sum for the marked path is 25.
Naive Solution
A naive solution for this challenge is to traverse all possible pathways and to calculate the sum for each one. By comparing the sum of the current pathway with the greatest sum for all previous pathways and keeping the greater value, you will eventually end up with the required answer. It's worth coding up this solution because describing all the pathways programmatically is a tidy challenge; however, this method will not satisfy the requirements of the task because it is impossible to analyse a triangle of more than ~30 rows on most computers. (If you get stuck trying to implement this solution, see this replit for one way to do it.)
The problem with the naive solution is that a triangle of \(n\) rows will require \(2^{(n-1)}(n-1)\) additions. This means that a 100-row triangle needs over \(6\times10^{31}\) operations. My computer can only do about 24 billion integer additions per second, so a 100-row triangle would take it about 80,000,000,000,000 years.
Evaluating algorithms in this way is an essential skill in computer science. Let's see how we arrive at the \(2^{(n-1)}(n-1)\) characterisation.
First, we count how many additions there are in each path. In Figure 1, we see that the marked path contains five numbers, and adding them together requires four separate addition operations: \[3 + 7 + 0 + 7 + 8 = 25 \] A moment's reflection should convince you that this will be true for any path in any triangle: there will be one number from each row, and there will be one fewer addition operations to get their sum. This gives us \((n-1)\) additions for each path in an n-row triangle.
Next, we count the number of paths in the triangle. In the example of a five-row triangle, we can see that there are two choices from the top number.
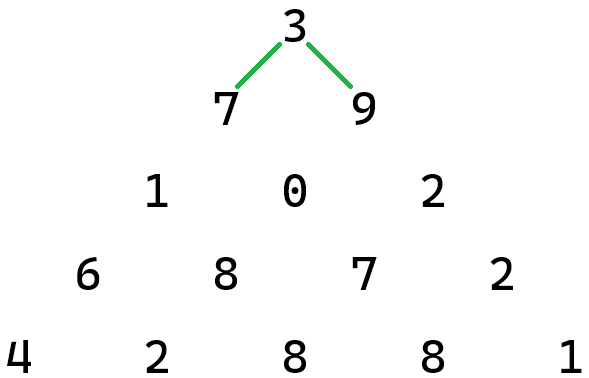
In the second row, there are again two choices from each number. This gives us \(2\times2=2^2\) paths from the top two rows.
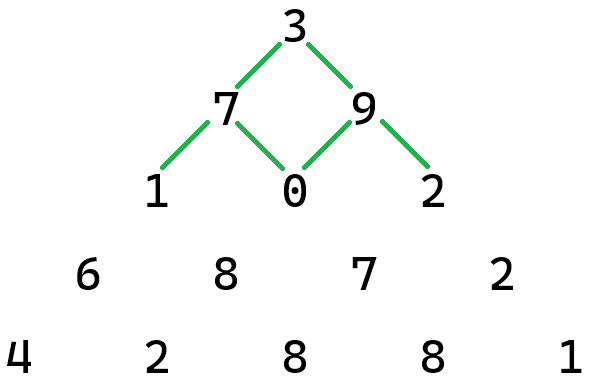
In the third row, it's a little harder to see all of the paths. It is true that you have two choices going forward from any number; however, you must remember that there are two ways to get to the zero. This means that there are actually four paths that go through zero, not two, and there are a total of eight paths through the top three rows. If you are having trouble seeing this, go to Figure 4 below and trace the following two paths that include the orange segment between the zero and the eight: 3 --> 7 --> 0 --> 8 and 3 --> 9 --> 0 --> 8. Similarly, there are two paths that include the orange segment between the zero and the seven on the fourth row. These are 3 --> 7 --> 0 --> 7 and 3 --> 9 --> 0 --> 7.
To find the number of paths from the top three rows, we can now add from left to right, starting with the segment from 1 --> 6. Each green segment appears in one path, while each orange segment appears in two paths. Thus there are \(1 + 1 + 2 + 2 + 1 + 1 = 8\) paths from the top three rows. We write this as \(2^{3}\).
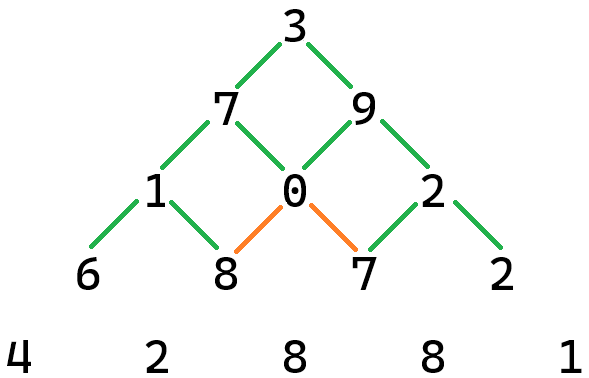
By now, you should be able to see that each of the purple segments in Figure 5 belongs to three different paths. This gives us sixteen paths from the top four rows, which is \(2^{4}\).
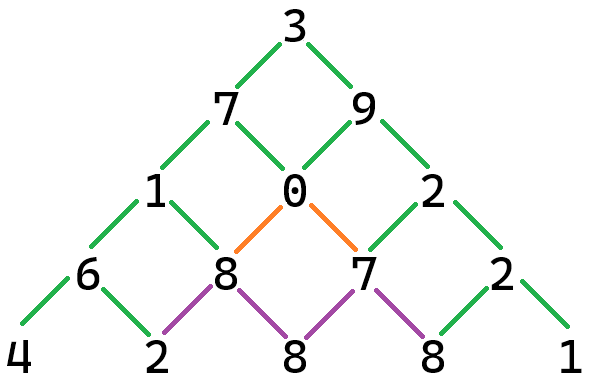
From the bottom row, there is nowhere else to go, so this triangle has sixteen paths. Summarising what we have seen, there are \(2^{1}\) paths from the first row to the second, \(2^{2}\) paths from the top to rows to the third, \(2^{3}\) paths from the top three rows to the fourth, and \(2^{4}\) paths from the top four rows to the fifth. In any number triangle we stop on the bottom row, so there are no paths from that row. This gives us \(2^{(n-1)}\) paths for a triangle with \(n\) rows.
With \((n-1)\) additions in each path, and \(2^{(n-1)}\) paths, we conclude that an n-row triangle requires \(2^{(n-1)}(n-1)\) additions.
Improved Solution
If the naive solution can't satisfy all the requirements in the problem statement, we need an improved solution. If we look at the paths taken in the naive solution, the problem with the algorithm quickly becomes obvious:
| 3 --> 7 --> 1 --> 6 --> 4 |
| 3 --> 7 --> 1 --> 6 --> 2 |
| 3 --> 7 --> 1 --> 8 --> 2 |
| 3 --> 7 --> 1 --> 8 --> 8 |
| \(\vdots\) |
| 3 --> 9 --> 2 --> 2 --> 1 |
Notice that the segment 3 --> 7 appears over and over (in fact, it appears in eight paths), meaning that the computer has to repeat the \(3 + 7\) operation unnecessarily. To improve the algorithm, we need to find a way to do each addition only once.
A slightly more clever way to look at the problem is to start from the bottom. In Figure 6, we can see that there are two paths that contain the 2 on the fourth row: 3 --> 9 --> 2 --> 2 --> 8 and 3 --> 9 --> 2 --> 2 --> 1.
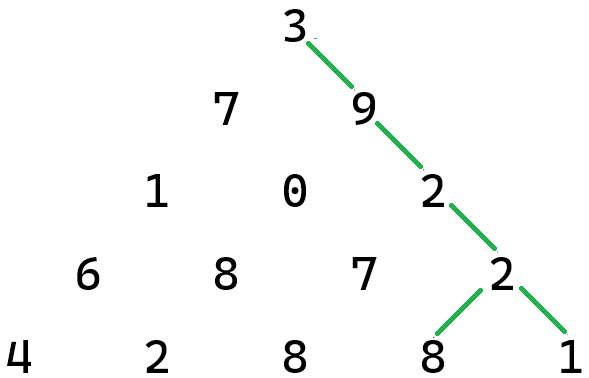
Of these, the path ending in 2 --> 8 has the larger sum, so the path ending in 2 --> 1 cannot possibly be the one we want, and we can safely ignore it. Further, the sum for the first path is exactly the same if we replace the 2 --> 8 segment with the sum \(2 + 8 = 10\).
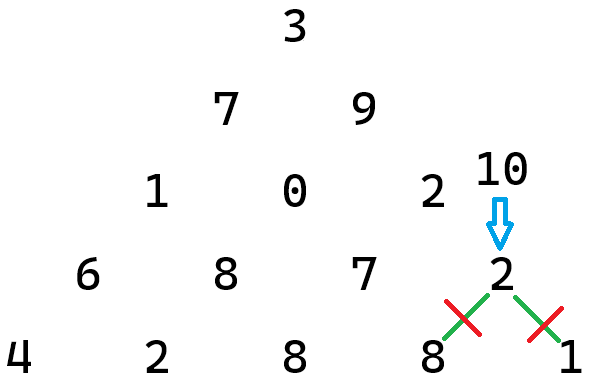
Looking next at the 7 in the fourth row, there are six paths that include this number (see Figure 5 above). None of their sums change if we replace the last segment of each with the sum \(7 + 8 = 15\). Continuing in this fashion, we can replace each number in the fourth row by the larger of the two sums that number makes with the numbers below it.
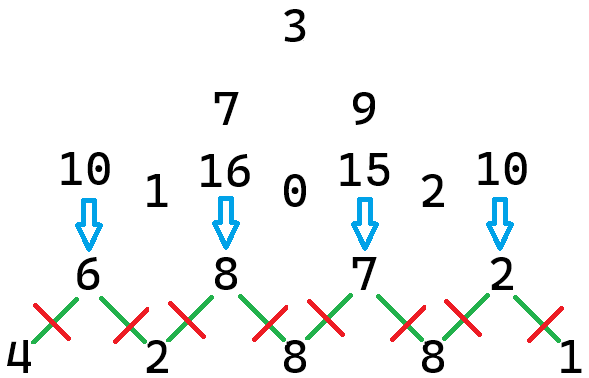
This process gives us a smaller triange that (for this task) is equivalent to the original.
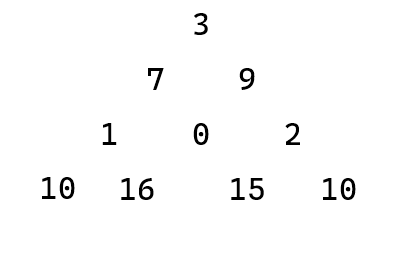
We next apply the strategy to the third row, replacing each of the numbers with the larger of the two sums the number makes with those below it.

The method continues in this fashion until it gives the largest sum, which replaces the number in the top row. In this case, that sum will be 29.
The question we must ask now is whether this "improved" method is any better than the naive solution. We might intuitively sense that it is because the method never adds the same two elements twice, but we can do better than intuition. We can calculate exactly the number of additions required for a triangle of \(n\) rows.
Going back to Figure 8, we see that the improved method required two additions for each of the elements on the fourth row. In terms of \(n\), this is \(2(n-1)\). Similarly, it required two additions for each element of the third row, which in terms of \(n\) is \(2(n-2)\). The second row required \(2(n-3)\) additions, and the first row, \(2(n-4)\). (Note that we did no additions starting from the nth row because no paths extend beyond that row.) We can summarise this as: \[2(n-1) + 2(n-2) + 2(n-3) + 2(n-4)\] the more customary way to write this sum is \[2(n-4) + 2(n-3) + 2(n-2) + 2(n-1) = \] \[2((n-4)+ (n-3) + (n-2) + (n-1))\] Finally, because this is from our \(n=5\) example, \[2(1 + 2 + \ldots + (n-1))\]
You may recognize the sum in brackets as being the \((n-1)^{th}\) triangular number. This means we can use the triangular number formula (Thanks, Carl Gauss!). That formula gives us \[2(1 + 2 + \ldots + (n-1)) = 2(\frac{n(n-1)}{2})=n(n-1)\]
So, is the "improved" method really an improvement? For a 100-row number triangle, the computer will have to do 9,900 integer additions rather than the \(6\times10^{31}\) required by the naive solution. Of course, we haven't fully characterised the algorithm (there are comparisons and memory operations that we haven't considered, for example), but we have proven the algorithm is better in terms of additions.
Next Steps
The analysis and characterisation of algorithms is a key part of computer science. This is a clear and interesting video from MIT's introductory course to get you started. If you prefer to read rather than watch (it's much faster for me), then an informal but good introduction can be found here and here.