Back

Analysis: A Splash of Milk

Nota Bene

There are a number of ways to do this problem almost (but not quite) correctly, so please use all of the test cases listed below to test your solution. When your program properly processes all of them, you can be reasonably sure it is correct.

Challenge

In this task , you are asked to determine how far a contaminant spreads given optimal (but limited) containment measures. Starting from a single contaminated house, the contaminant will spread every hour to the immediate neighbours of all previously contaminated houses. Every house (except the first) may have between one and three neighbours, so there is the possibility of up to \(2^{n}\) newly-contaminated houses (one neighbour will already have been contaminated) at hour \(n\). The containment strategy is to isolate one house each hour from all its neighbours, just before the contamination spread is updated.

The example configuration of houses given in the problem statement is shown in its uncontaminated state in Figure 1 below.

Figure 1 - Uncontaminated State

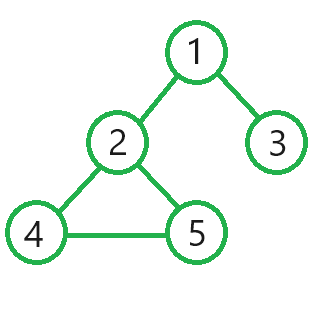
Initially, house one is contaminated. This puts houses two and three in danger of contamination when the next hour begins. This is shown in Figure 2.

Figure 2 - Initial Contamination

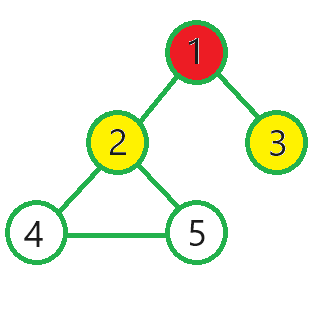
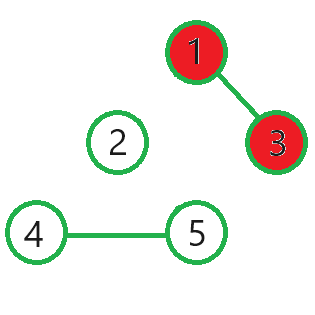
You can isolate one of these houses before the contamination can reach it. By choosing to isolate house two, you limit the total contamination to two houses. Figure 3 shows the situation at that point.

Figure 3 - Final State after Containment

The organisers of the 2023 BIO mean for you to model this task as a graph. There are conventions for programmatically representing graphs, and graph problems deserve to be treated as their own genre. If you have not programmed graph problems before, you may wish to try the Beginner Zone challenges related to graphs first. If you intend to compete, you must learn how to work with graphs without using secondary libraries such as NetworkX (Python) or Boost Graph Library (C++). They are not part of the standard library set, and you will not have access to them on competition platforms.

Solution Strategy

For me, this problem required a bit of pencil-and-paper analysis before I began coding. By finding counter-examples (cases where a particular approach would not work), I could quickly rule out a number of strategies. Here is the solution I came up with, using recursion:

  1. Determine how many new nodes would be contaminated if the current node becomes contaminated.
    1. Exclude from consideration all the nodes along the path from the root to this node. (They have to be contaminated already.)
    2. Exclude from consideration any other neighbours of this node's parent, if there are any. (The parent is the node immediately prior to this one on the path from the root. If this node is contaminated, the other neighbour has to have been isolated.)
    3. If there are zero or one non-excluded neighbours, the answer for this node is 1. Continue to step 2. (If this node has only one non-excluded neighbour, it will be isolated.)
    4. For each of the non-excluded neighbors in turn, make it the current node and get its "would be contaminated score" by starting at step 1.
    5. The highest-scoring neighbour will be isolated, so ignore its score and total the scores from all the other neighbours.
    6. Add one to the total from 1.e. to indicate that this node will also be contaminated. This is the answer for this node; continue to step 2.
  2. Unless this node is the root, return the total found in step 1 to this node's parent. If this is the root, the total is the score for the graph.

Be especially careful about which nodes are excluded. If your program is not passing the test vectors, you may have excluded the wrong ones or failed to exclude some nodes. Pictures help a lot!

Test Vectors

Vector Expected Score
data1 2
data2 3
data3 3
data4 3
data5 5
data6 11

Next Steps

Graph theory has broad application not only to computer science but also to a number of important subdomains in engineering, business, and public health. It is also an interesting context for the application of combinatorics, probability, and abstract algebra. You can learn more from these sources: